
I hope these examples have helped you to understand the quotient rule and one more method of differentiation as part of your journey through calculus. This equation can easily be divided and you can then just simply use the power rule which would be much faster and easier. An example of this equation would be y=(x^2+x)/(x).
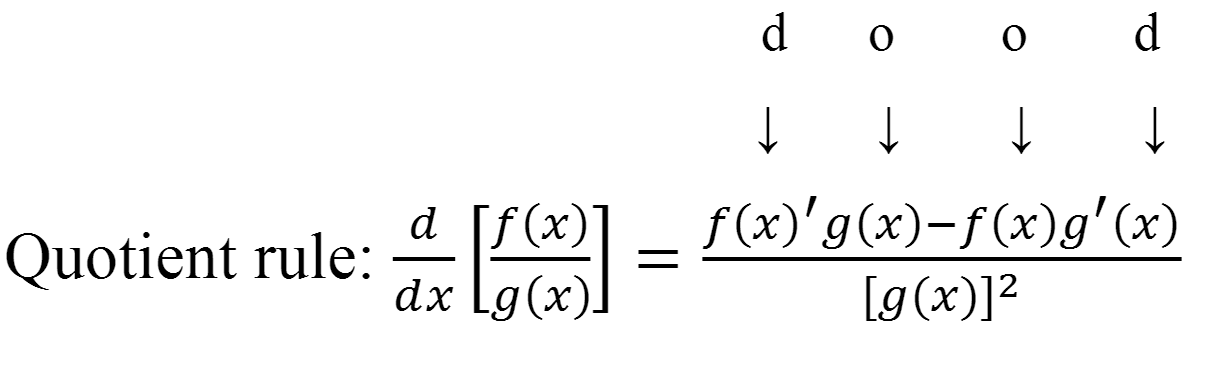
One last thing to note is that the quotient rule shouldn’t be used if it is easy to divide. This saying is “low dee high minus high dee low over low squared”.Now that we have completed an example together, this saying should make more sense and make it easier for you to calculate using the quotient rule. Continuity), Derivatives (Basic Formulas, Product/Quotient/Chain Rules. This should simplify to (x^4-6x^3-4x^2-2x+3)/((x-3)^2(x^2)).Īn easy way to remember the formula is through a specific mnemonic saying. The differentiation calculator shows possible intermediate steps, plots, roots. Then, you divide the difference by the square of g(x) which would be (x^2-3x)^2. Then you subtract the result by the product of f(x) being (x^3+4x+1) and the derivative of g(x) being (2x-3).
QUOTIENT RULE CALCULUS LOW FREE
For the graph of f (x), Vertex (0, 0) Solve your math problems using our free math solver with. We first multiply g(x) being (x^2-3x) and the derivative of f(x) which is (3x^2+4). Explanation: Assuming that those who are reading have a minimum level in Maths, everyone knows perfectly that the quotient rule is color (blue) ( ( (u (x))/ (v (x)))' (u' (x)v (x)-u (x)v' (x))/ ( (v (x)))), where u (x) and v (x) are functions and u' (x), v' (x) respective derivates. Basic Differentiation Rules For Derivatives. This might sound like a mouthful, so I will provide you with an example.įor an example of this quotient rule, let's use the equation y=((x^3+4x+1)/(x^2-3x)). In this specific formula, you are supposed to take the derivative of f(x) and multiply it by the expression g(x), and then subtract it by the product of the derivative of g(x) and the expression f(x), and then finally divide the entire result by the square of g(x). So, What is the quotient rule? Well, first, let's define the top expression as f(x) and the bottom expression as g(x). So, the quotient rule could make the process of finding the derivative easier in these types of functions. In some cases, you might be able to divide the function and use the power rule, but in these cases, it might take longer to divide and you might end up with a remainder which would be usually hard to deal with. An example of such an equation would be y=((x^3+4x+1)/(x^2-3x)). The quotient rule is used to differentiate a function in which one expression is divided by another. The quotient rule is another method of solving more complex functions. You can clean it up if you wish, but most teachers will be okay if you leave it here, you may also factor a bit if you would like.In the next topic in our exploration of derivatives, we will be talking about the concept of the quotient rule. these are designed to retain thick lubricant at low pressure in motors, pumps. Now this lovely function is your second derivative. 52 X 2Once you complete the multiplication follow these two rules. Now we must find the derivative of this, having fun yet? We take the denominator times the derivative of the numerator (low d-high). Non-calculator derivatives are typically less complex than those that require numerical derivatives. Which simplifies to ( Going to go ahead and put the derivatives here): quotient rule calculus fractionDerivatives of Rational Functions Brilliant. Exam Insights The Quotient Rule is present throughout all sections of the exam. Now in order to find the second derivative, you must take the derivative of the first derivative, but I'm going to clean it up first. Now this expression above is your first derivative. Now that we have that, we plug in each value into the quotient rule.
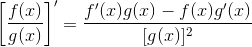
We find the derivatives of the numerator and denominator using the power rule. by cancelling the factor of x in the numerator and the denominator. So, if we write down the function next to it's derivatives, it would look like this: So the denominator times the derivative of the numerator minus the numerator times the derivative of the denominator divided by the denominator squared. The quotient rule goes as follows: #dy/dx f(x)/g(x) = (g(x)f'(x)-f(x)g'(x))/g(x)^2#Īn easy way to remember this is the mnemonic "low d hi - hi d low over low squared." D meaning derivative.


 0 kommentar(er)
0 kommentar(er)
